Trigonometrian ymmärtämiseksi matematiikkaan on suhtauduttava uusilla näkökulmilla. Tämän näkökulman tunnistaminen voi olla tuskallista, mutta nautittavaa. Jos tarkastelet matematiikkaa peloissaan ja epävarmuudessa, tämä artikkeli auttaa toivottavasti tulemaan optimistisemmaksi trigonometrialuokan aloittamisessa.
Monimutkainen logiikka on esitetty
Kun tulevat college, en saanut matematiikkaa. Vaikka tieteet kiinnostivat minua, juoksin heiltä kirjallisuuden ja filosofian käsivarsiin, jotta minun ei tarvitse kohdata neljää lukukautta lukukautta. Mutta viimeisellä lukukaudella perustutkintoni ilmoittautuin matemaattisesti perustuvaan filosofian luokkaan. Olin hämmästynyt esitetystä monimutkaisesta logiikasta. Etsin tapaa jakaa kukin ongelma alkeellisimpiin osiin ja sitten koota ne ratkaisun luomiseksi.
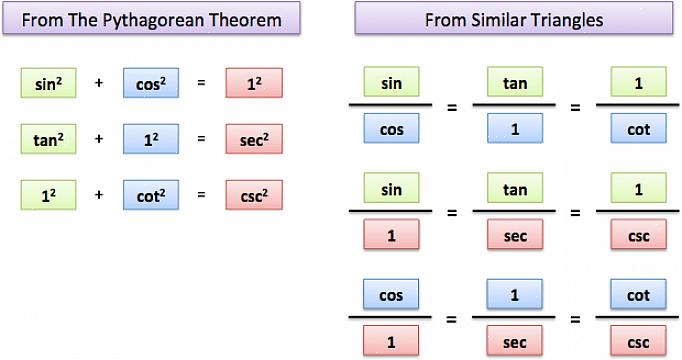
Avain trigonometrian ymmärtämiseen on muistaa, että matematiikka noudattaa yksinkertaista sääntöjoukkoa. Trigonometrian periaatteet perustuvat pisteiden suhteen selvittämiseen ympyrässä. Saadaksesi ympyrän x-akselin, käytä siniä ja funktiota sinus = y-akselin pituus / hypotenuus. Kosini = x-akseli / hypotenuusaa, ja tangentti on kuvioitu käyttäen Pythagoraan lauseen. Kun nämä säännöt on ymmärretty, siitä tulee yksinkertainen logiikkasääntöihin perustuva rakenne. Tässä asetetaan matematiikkaan sisältyvä luovuus.
Ratkaista ongelmia
Murtamalla sinin, kosinin ja tangentin yksinkertaisemmaksi kieleksi ja oppimalla, kuinka voimme soveltaa näitä kaavoja käytännöllisesti sen sijaan, että ajattelisimme niitä vain käsitteiksi, joihin olemme juuttuneet luokkahuoneessa, voimme alkaa havaita niiden toiminnan ja alkaa ymmärtää kuinka käyttää trigonometriaa ongelmien ratkaisemiseen.
Jos opetin murto-osia lapsille, näytän heille 8 viipaleeksi leikatun pizzan. Poistaisin sitten pizzan osat ja kysyin opiskelijalta, kuinka paljon meillä oli jäljellä koko pizzasta. Lapset ymmärtäisivät poikkeuksetta tämän käsitteen nopeammin kuin kuvailisin vain murto-osia ilman vertailupistettä. Samoin meidän on visualisoitava trigonometristen järjestelmien hyödyllisyys niiden ymmärtämiseksi. Muista kuusi peruskaavaa tämä kolmio mielessä. Nämä ovat trigonometrian elementtejä.
Sinulla on vaikeuksia ymmärtää trigonometriaa. Työskentele opettajien ja opettajien kanssa selvittääksesi, miten trigonometrian perusperiaatteita voidaan soveltaa omaan elämään. Kun trigonometriaa voidaan soveltaa jokapäiväiseen elämään, oppiminen on helpompaa. Matematiikka voi olla hauskaa, jos ymmärrät sen luovuuden. Työskentele ahkerasti trigonometrian ymmärtämiseksi ja saat käsityksen täysin erilaisesta ajatusmaailmasta.